The equation of the line is given as
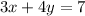
The general equation of a line is
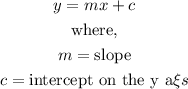
Step 1: Make y the subject of the formula
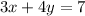
Subtract 3x from both sides
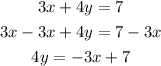
Step 2: Divide all through by 4
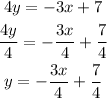
Step 3 : Compare coefficients with the general equation of a line below
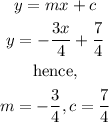
For a perpendicular line,
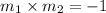
That is, we will have that
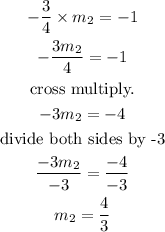
Hence,
The slope of the perpendicular line will be = 4/3
For a parallel line,
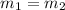
Therefore,
The slope of a parallel line will be = -3/4