Question

A Hatbox, in the shape of a circular cylinder, is to be constructed in such a manner that the sum of its height and the radius is 9 units. What is the radius largest volume?

Answer 1

Given:

The sum of the radius and height of the cylinder is 9 units.

To find the largest volume:

Since sum of the radius and height of the cylinder is 9 units.

`\begin{gathered} r+h=9 \\ h=9-r\ldots\ldots\ldots\ldots(1) \end{gathered}`

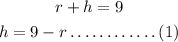
The formula of volume of the cylinder is,

`\begin{gathered} V=\pi r^2h \\ =\pi* r^2*(9-r) \\ V=\pi(9r^2-r^3)\ldots\ldots\ldots\ldots(2) \end{gathered}`

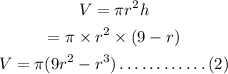
To find the maximum of the function:

Differentiate with respect to r,

`\begin{gathered} (dV)/(dr)=0 \\ \pi(18r-3r^2)=0 \\ 18r-3r^2=0 \\ 3r\text{(6-r)=0} \\ r=0,r=6 \end{gathered}`

It is impossible that r=0.

So, let us substitute r=6 in equation (2) we get,

`\begin{gathered} V=\pi(9(6)^2-6^3) \\ =\pi(324-216) \\ =108\pi \\ =108*(22)/(7) \\ \approx339.43\text{ cubic units} \end{gathered}`

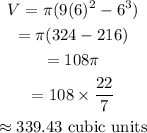
Hence, the largest volume of the cylinder is 339.43 cubic units.