Given:
Height of cylinder, h = 9 cm
Radius, r = 3 cm
Total amount of paper the company has = 8138.88 cm²
Let's find the number of labels that can be made given that the label covers only the side.
Here, we are to apply the formula for the surface area of a cylinder.
We have:
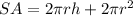
The 2πr² represents the area of the top and bottom circle of the cylinder.
Since the label covers only the side, we are to exclude the 2πr².
Hence. we have:
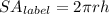
WHere:
r = 3 cm
h = 9 cm
Thus, we have:
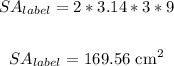
Now, the number of labels they can make is:
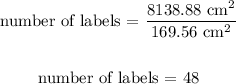
Therefore, the company can make 48 labels.
ANSWER:
48 Labels