Question

A company makes paper labels for paint cans. As shown below, cach can is in the shape of a cylinder with a height of 9 cm and a radius of 3 cm. The paper labelis wrapped around the can and covers only the side of the can (not the top or bottom). If the company has a total of 8138.88 cm^2 or paper available, how manylabels can be made? Use 3.14 for x, and do not round your answer.

Answer 1

Given:

Height of cylinder, h = 9 cm

Radius, r = 3 cm

Total amount of paper the company has = 8138.88 cm²

Let's find the number of labels that can be made given that the label covers only the side.

Here, we are to apply the formula for the surface area of a cylinder.

We have:

`SA=2\pi rh+2\pi r^2`

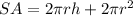
The 2πr² represents the area of the top and bottom circle of the cylinder.

Since the label covers only the side, we are to exclude the 2πr².

Hence. we have:

`SA_(label)=2\pi rh`

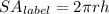
WHere:

r = 3 cm

h = 9 cm

Thus, we have:

`\begin{gathered} SA_(label)=2*3.14*3*9 \\ \\ SA_(label)=169.56\text{ cm}^2 \end{gathered}`

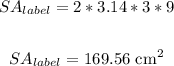
Now, the number of labels they can make is:

`\begin{gathered} \text{ number of labels = }\frac{8138.88\text{ cm}^2}{169.56\text{ cm}^2} \\ \\ \text{ number of labels = 48} \end{gathered}`

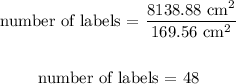
Therefore, the company can make 48 labels.

ANSWER:

48 Labels