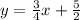Question

Find equation of the tangent to x2 +xy + 2y3 = 4 at (– 2, 1).

Answer 1

Given:

`x^2+xy+2y^3=4`

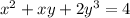
Let's find the equation of the tangent to the given equation at the point:

(x, y) ==> (-2, 1)

Let's first find the derivative of the given equation.

We have:

`\begin{gathered} (d)/(dx)(x^2+xy+2y^3)=(d)/(dx)(4) \\ \\ 2x+y+xy^(\prime)+6y^2y^(\prime)=0 \end{gathered}`

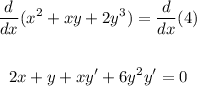
Now, rewrite the equation for y':

`\begin{gathered} xy^(\prime)+6y^2y^(\prime)=-2x-y \\ \\ \text{ Factor out y':} \\ y^(\prime)(x+6y^2)=-2x-y \\ \\ \text{ Divide both sides by \lparen x}+6y^2): \\ (y^(\prime)(x+6y^2))/(x+6y^2)=(-2x-y)/(x+6y^2) \\ \\ y^(\prime)=(-2x-y)/(x+6y^2) \\ \\ y^(\prime)=-(2x+y)/(x+6y^2) \end{gathered}`

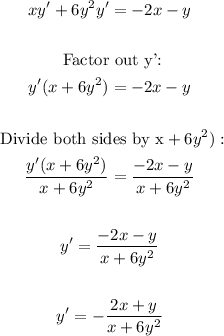
Now, to find the slope of the tangent, evaluate the derivative at the point (-2, 1).

Substitute -2 for x and 1 for y:

`\begin{gathered} m=-(2(-2)+1)/(-2+6(1)^2) \\ \\ m=-(-4+1)/(-2+6) \\ \\ m=-(-3)/(4) \\ \\ m=(3)/(4) \end{gathered}`

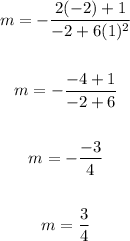
The slope of the tangent line is 3/4.

Now, to find the equation of the tangent line, apply the point-slope form:

`y-y_1=m(x-x_1)`

Plug in -2 for x1 and 1 for y1 and 3/4 for m:

`\begin{gathered} y-1=(3)/(4)(x-(-2)) \\ \\ y-1=(3)/(4)(x+2) \\ \\ y-1=(3)/(4)x+(3)/(4)*2 \\ \\ y-1=(3)/(4)x+(3*2)/(4) \end{gathered}`

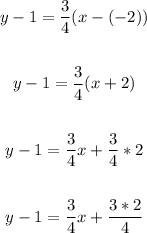
Solving further:

`\begin{gathered} y-1=(3)/(4)x+(6)/(4) \\ \\ y-1=(3)/(4)x+(3)/(2) \\ \\ Add\text{ 1 to both sides:} \\ y-1+1=(3)/(4)x+(3)/(2)+1 \\ \\ y=(3)/(4)x+(3+2)/(2) \\ \\ y=(3)/(4)x+(5)/(2) \end{gathered}`

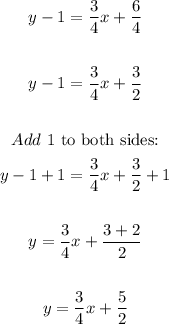
Therefore, the equation of the tangent line is:

`y=(3)/(4)x+(5)/(2)`

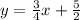
• ANSWER:

`y=(3)/(4)x+(5)/(2)`