Read image for instructions Answer choices A. 271B. 423C. 651D. 888

Question

asked Jun 28, 2023 181k views

1 Answer

Smehmood · Answer 1 · 2023-07-02T16:34:24+0000

We are asked to find the required sample size for a proportion.

Given information:

Margin of error = 4% = 0.04

Confidence level = 90% = 0.90

Significance level = 1 - 0.90 = 0.10

The two-sided z-score corresponding to α = 0.10 is found to be 1.645

The required sample size is given by

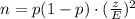
$n=p(1-p)\cdot((z)/(E))^2$

Where p is the estimated proportion and can be assumed to be 0.50 when it is not given.

z is the z-score and E is the margin of error

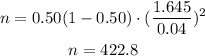
$\begin{gathered} n=0.50(1-0.50)\cdot((1.645)/(0.04))^2 \\ n=422.8 \end{gathered}$

Round up the answer to a whole number.

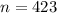
Therefore, the smallest sample size required to obtain the desired margin of error is 423