Question

ALGEBRA 2: $7,700 is invested in an account earning 7.3% interest (APR), compounded daily.Write a function showing the value of the account after t years, where the annual growth rate can be found from a constant in the function. Round all coefficients inthe function to four decimal places. Also, determine the percentage of growth peryear (APY), to the nearest hundredth of a percent.

Answer 1

Given:

Part A:

`\begin{gathered} P=\text{ \$7,700} \\ r=7.3\text{ \%}=(7.3)/(100)=0.073 \\ n=365...............compounded\text{ daily} \end{gathered}`

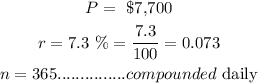
Using the compound interest formula,

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ \\ Thus, \\ A=7700(1+(0.073)/(365))^(365* t) \\ A=7700(1+0.0002)^(365t) \\ A=7700(1.0002)^(365t) \end{gathered}`

Therefore, the function showing the value of the account after t-years is:

`A=7700(1.0002)^(365t)`

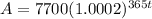
Part B:

To get the percentage growth per year, we get the amount in the account at the end of two successive years.

At the end of year 1:

`\begin{gathered} A=7700(1.0002)^(365t) \\ \\ when\text{ }t=1 \\ A=7700(1.0002)^(365*1) \\ A=7700(1.0002)^(365) \\ A=\text{ \$}8283.06 \end{gathered}`

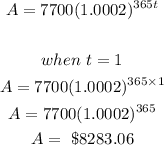
At the end of year 2:

`\begin{gathered} A=7700(1.0002)^(365t) \\ \\ when\text{ }t=2 \\ A=7700(1.0002)^(365*2) \\ A=7700(1.0002)^(730) \\ A=\text{ \$}8910.28 \end{gathered}`

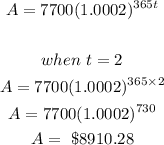
The percentage growth is gotten using the formula:

`\begin{gathered} PGR=(\frac{Ending\text{ value}}{Beginning\text{ value}}-1)*100\text{ \%} \\ PGR=((8910.28)/(8283.06)-1)*100\text{ \%} \\ PGR=(1.0757-1)*100\text{ \%} \\ PGR=0.0757*100\text{ \%} \\ PGR=7.57\% \end{gathered}`

Therefore, the percentage of growth per year (APY) is 7.57%