Solution:
Given:
Part A:
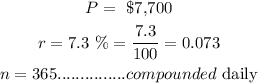
Using the compound interest formula,

Therefore, the function showing the value of the account after t-years is:
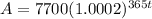
Part B:
To get the percentage growth per year, we get the amount in the account at the end of two successive years.
At the end of year 1:
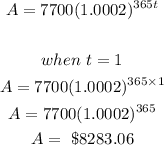
At the end of year 2:
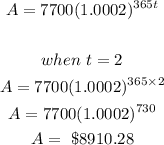
The percentage growth is gotten using the formula:

Therefore, the percentage of growth per year (APY) is 7.57%