SOLUTION
We want to find the principal money borrowed each at 13% and 15% from a total money of $25,000.
Now, let the money he borrowed at 15% be x
and, let the money he borrowed at 13% be y.
This means that
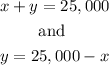
From the simple interest formula
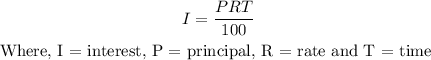
Interest on 15% will be
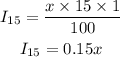
Interest on 13% will be
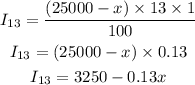
Now, both interest should be = $3,600
That is
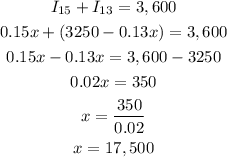
So, the money he borrowed at 15% is $17,500
And the money he borrowed at 13% is
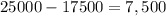
Hence, the answer is $17,500 at 15% and $7,500 at 13%.