Question

John barley borrowed $25,000 for one year he borrowed some at 13% interest and the rest at 15% interest at the end of the year he owed $3,600 in interest how much did he borrow at each rate.?

Answer 1

We want to find the principal money borrowed each at 13% and 15% from a total money of $25,000.

Now, let the money he borrowed at 15% be x

and, let the money he borrowed at 13% be y.

This means that

`\begin{gathered} x+y=25,000 \\ \text{and } \\ y=25,000-x \end{gathered}`

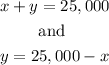
From the simple interest formula

`\begin{gathered} I=(PRT)/(100) \\ \text{Where, I = interest, P = principal, R = rate and T = time } \end{gathered}`

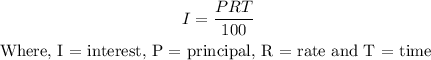
Interest on 15% will be

`\begin{gathered} I_(15)=(x*15*1)/(100) \\ I_(15)=0.15x \end{gathered}`

Interest on 13% will be

`\begin{gathered} I_(13)=((25000-x)*13*1)/(100) \\ I_(13)=(25000-x)*0.13 \\ I_(13)=3250-0.13x \end{gathered}`

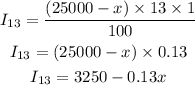
Now, both interest should be = $3,600

That is

`\begin{gathered} I_(15)+I_(13)=3,600 \\ 0.15x+(3250-0.13x)=3,600 \\ 0.15x-0.13x=3,600-3250 \\ 0.02x=350 \\ x=(350)/(0.02) \\ x=17,500 \end{gathered}`

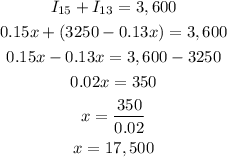
So, the money he borrowed at 15% is $17,500

And the money he borrowed at 13% is

`25000-17500=7,500`

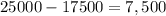
Hence, the answer is $17,500 at 15% and $7,500 at 13%.