Question

Suppose the coefficient of kinetic friction between mA and the plane in the figure(Figure 1) is μk = 0.15, and that mA=mB=2.7kg. a is doneAs mB moves down, determine the magnitude of the acceleration of mA and mB, given θ = 30 ∘ans 1.8 m/s2bWhat smallest value of μk will keep the system from accelerating?

Answer 1

Given:

The coefficient of friction between the plane and the mass A is,

`\mu_k=0.15`

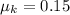
The masses are,

`m_A=m_B=2.7\text{ kg}`

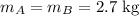
The angle of inclination is,

`\theta=30\degree`

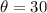
To find:

a) the acceleration of the masses

b) The smallest value of the coefficient of friction which will keep the system from accelerating

Step-by-step explanation:

a)

The free-body diagram is:

For the mass B,

`m_Ba=m_Bg-T`

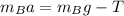
For the other mass, the normal reaction is,

`N=m_Agcos\theta`

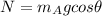
Again the horizontal motion gives,

`\begin{gathered} m_Ba=T-f-m_Bgsin\theta \\ m_Ba=T-\mu_km_Bgcos\theta-m_Bgs\imaginaryI n\theta \end{gathered}`

Combining the equations we get,

`\begin{gathered} a=(m_Bg-m_Agsin\theta-\mu_km_Agcos\theta)/(m_A+m_B) \\ =(2.7*9.8-2.7*9.8* sin30\degree-0.15*2.7*9.8* cos30\degree)/(2.7+2.7) \\ =1.8\text{ m/s}^2 \end{gathered}`

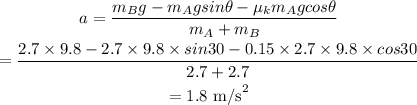
Hence, the acceleration is,

`1.8\text{ m/s}^2`

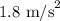
b)

For, the zero acceleration,

`\begin{gathered} a=(m_(B)g-m_(A)gs\imaginaryI n\theta-\mu_(k)m_(A)gcos\theta)/(m_(A)+m_(B))=0 \\ m_B-m_As\imaginaryI n\theta-\mu_km_Acos\theta=0 \\ \mu_k=\frac{m_B-m_As\mathrm{i}n\theta}{m_Acos\theta} \\ \mu_k=(2.7-2.7* sin30\degree)/(2.7cos30\degree) \\ \mu_k=0.58 \end{gathered}`

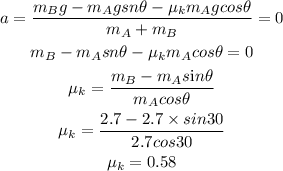
Hence, the required kinetic friction is 0.58.