Given:
The coefficient of friction between the plane and the mass A is,
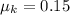
The masses are,
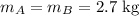
The angle of inclination is,
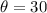
To find:
a) the acceleration of the masses
b) The smallest value of the coefficient of friction which will keep the system from accelerating
Step-by-step explanation:
a)
The free-body diagram is:
For the mass B,
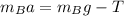
For the other mass, the normal reaction is,
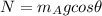
Again the horizontal motion gives,
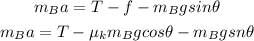
Combining the equations we get,
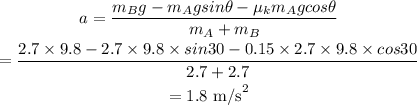
Hence, the acceleration is,
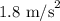
b)
For, the zero acceleration,
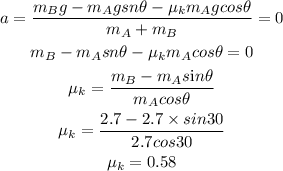
Hence, the required kinetic friction is 0.58.