Question

The age of U.S. millionaires is normally distributed with a standard deviation o = 13.0years. A group of 36 millionaires is randomly selected and their mean age is & = 58.5years old. Construct a 95% confidence interval for the mean age of U.S. millionaires.

Answer 1

The 95% confidence interval for the mean age of U.S. millionaires, given a sample mean age of 58.5 years, a standard deviation of 13.0 years, and a sample size of 36, is between 54.3 and 62.7 years old.

Step-by-step explanation:

To construct a 95% confidence interval for the mean age of U.S. millionaires, we use the given standard deviation (σ = 13.0 years), the sample mean (&x0305; = 58.5 years), and the sample size (n = 36). Since the sample size is larger than 30, we can use the z-distribution for the confidence interval.

The formula for a confidence interval is given by:

Confidence Interval = &x0305; ± z * (σ / √n)

First, we find the z-score for a 95% confidence level. The z-score that corresponds to a 95% confidence level is approximately 1.96.

Now we can calculate the confidence interval:

Margin of Error (ME) = z * (σ / √n) = 1.96 * (13.0 / √36) ≈ 4.2

Therefore, the confidence interval is:

58.5 ± 4.2 = (54.3, 62.7)

This means we can be 95% confident that the true mean age of U.S. millionaires is between 54.3 and 62.7 years old.

Answer 2

a) Parameter, population standard deviation σ = 13.0

__

Sample statistics n=36 x = 58.5

b)The margin of error E is 4.2467

c)The confidence interval is (54.2533, 62.7467)

d) we are 95% confident that the mean age of US millionaires is between (54.2533 , 62.7467)

EXPLANATION

From the given question;

a) The given Parameter or (statistics)

Parameter, population standard deviation σ = 13.0

__

Sample statistics n=36 x =58.5

b) The margin of Error E can be calculated using the formula below:

`M.E=Z_{(\propto)/(2)}*\frac{\sigma}{\sqrt[]{n}}`

Substitute the the values into the formula and simplify.

`=1.96*\frac{13}{\sqrt[]{36}}`

`=1.96*(13)/(6)`

`=(25.48)/(6)`

`=4.2467`

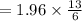
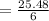
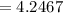
Hence, the margin of error E is 4.2467

c) The confidence interval can be calculated using the formula below:

`C.I=\bar{x}\text{ }\pm Z_{\propto\text{ /2}}*\frac{\sigma}{\sqrt[]{n}}`

`This\text{ implies; C.I = mean age }\pm\text{ margine error}`

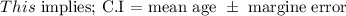
Substitute the values and simplify.

`C\mathrm{}I=58.5\pm4.2467`

`C.I=(54.2533,\text{ 62.7467)}`

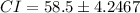
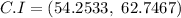
Hence, the confidence interval is (54.2533, 62.7467)

d)Conclusion

Hence, we are 95% confident that the mean age of US millionaires is between (54.2533 , 62.7467)