a) Parameter, population standard deviation σ = 13.0
__
Sample statistics n=36 x = 58.5
b)The margin of error E is 4.2467
c)The confidence interval is (54.2533, 62.7467)
d) we are 95% confident that the mean age of US millionaires is between (54.2533 , 62.7467)
EXPLANATION
From the given question;
a) The given Parameter or (statistics)
Parameter, population standard deviation σ = 13.0
__
Sample statistics n=36 x =58.5
b) The margin of Error E can be calculated using the formula below:
![M.E=Z_{(\propto)/(2)}*\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/7wyy46pjnq4jcxn343wjzplrkeruhxth66.png)
Substitute the the values into the formula and simplify.
![=1.96*\frac{13}{\sqrt[]{36}}](https://img.qammunity.org/2023/formulas/mathematics/college/9d0va1mlcwhqquksja7qmb70d41xc2idjf.png)

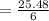

Hence, the margin of error E is 4.2467
c) The confidence interval can be calculated using the formula below:
![C.I=\bar{x}\text{ }\pm Z_{\propto\text{ /2}}*\frac{\sigma}{\sqrt[]{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/louwl1cfjp38yeypj1y18er8uu5koxogtj.png)

Substitute the values and simplify.
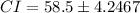
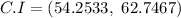
Hence, the confidence interval is (54.2533, 62.7467)
d)Conclusion
Hence, we are 95% confident that the mean age of US millionaires is between (54.2533 , 62.7467)