Question

Question shown in the photo, don’t mind the unfinished answer in the text box

Answer 1

Since the production of y must exceed the production of x by at least 100 units, we can write a second inequality:

`y\ge x+100`

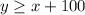
Looking at the function P, we can see that the coefficient multiplying y is greater than the coefficient multiplying x, therefore increasing y instead of x will have a bigger increase in P.

But from the inequality x + 2y <= 1400, we can see that the "cost" of producing y is two times the "cost" of producing x, that is, for one y produced, we could have produced 2x instead.

The coefficient of y is greater, but it's not more than 2 times greater, therefore it's better to produce x than y.

Since y needs to be at least 100 more than x, let's choose the minimum amount of y to satisfy the inequalities:

`\begin{gathered} x+2y\le1400\to x\le1400-2y \\ x+100\le y\to x\le y-100 \\ \\ 1400-2y=y-100 \\ y+2y=1400+100 \\ 3y=1500 \\ y=500 \\ x+100=500 \\ x=400 \end{gathered}`

Therefore the values of x and y that give the maximum profit are x = 400 and y = 500.

Graphing the two inequalities, we have:

The feasible region is the intersection region (between red and blue).

The vertices are:

(0, 100), (400, 500), (0, 700).

Calculating the maximum profit (with vertex (400, 500)), we have:

`\begin{gathered} P=14\cdot400+22\cdot500-900 \\ P=5600+11000-900 \\ P=15700 \end{gathered}`

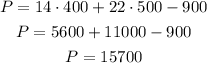
Therefore the production that yields the maximum profit is x = 400 and y = 500, and the maximum profit is P = 15700.