Given:
Function is
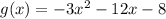
To find:
Write function in the form

Then give its vertex.
Step-by-step explanation:
We will try to make perfect square of terms.
vertex of
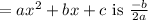
Solution:
We will solve equation by first making perfect square of terms as:
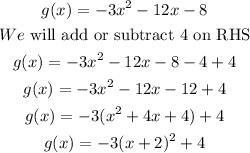
Now, vertex is
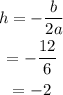
Now,
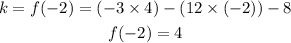
So, vertex is (-2, 4).
Hence , these are the answers.