The Solution:
For Mike's Repair charges, the equation:

For Sam's Repair charges, the equation is given as:
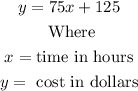
Part (a):
Comparing the total charges for a 2-hour job, we have
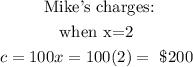
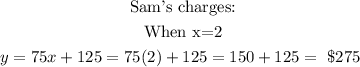
Clearly, we have that:
![\begin{gathered} cThus, <strong>the company that charges less for a 2-hour job is Mike's Repair which charges $200.</strong><p>Therefore, <strong>the correct answer is Mike's Repair.</strong></p><p>part (b):</p><p>To use my understanding of tables, graphs and equations to explain why I chose my answer in part (a):</p><p>The fixed charge of $125 by Sam's Repair accounted for his charges,</p><p>But Mike's Repair charges $0 as a fixed charge. Hence, the reduced charges especially when the number of hours for the job is less.</p>[tex]\begin{gathered} 75x+125\leq100x \\ 75x-100x\leq-125 \\ -25x\leq-125 \end{gathered}]()
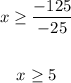
So, the charges for both Repairs can only be equal if the number of hours is 5.