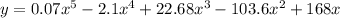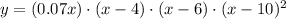
The standard form of a polynomial is given by the order of the terms making sure that the term with the highest degree is placed first.
start expanding the square term
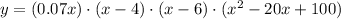
then, multiply the first two terms
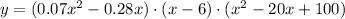
continue multiplying the next two terms
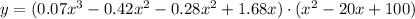
simplify and organize the terms
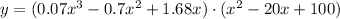
solve the final product
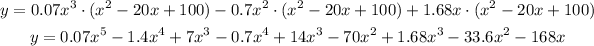
group alike terms