Question

John and Susan can clean their house in 5 hours. Working alone, Susan can clean the house one hour faster than John can clean the house. How long does it take each person to clean the house alone?

Answer 1

Let J be the time (in hours) John takes to clean the house alone, and S be the time (in hours) Susan takes to clean the house alone since they can clean the house in 5 hours together, and Susan can clean the house one hour faster than John, then we can set the following system of equations:

`\begin{gathered} (1)/(S)\cdot5+(1)/(J)\cdot5=1, \\ S=J-1. \end{gathered}`

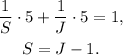
Substituting the second equation in the first one we get:

`(5)/(J-1)+(5)/(J)=1.`

Multiplying the above equation by (J-1)J we get:

`((5)/(J-1)+(5)/(J))*((J-1)J)=1*(J-1)J\text{.}`

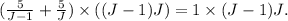
Simplifying the above equation we get:

`\begin{gathered} (5)/(J-1)*(J-1)J+(5)/(J)*(J-1)J=(J-1)J, \\ 5J+5(J-1)=J^2-J, \\ 10J-5=J^2-J\text{.} \end{gathered}`

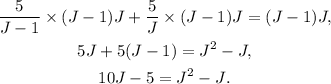
Solving the above equation for J we get: