Question

M is the midpoint of JK. The coordinates of J are (6, 3) and the coordinates of M are (-3, 4) find the coordinates of K.

Answer 1

Given the line segment JK, point M is its midpoint, this means that it divided the line segment in two smaller segments of equal size:

JM=MK

JK= JM+MK

Since the distance from J to M is the same as the distance from M to K, first step is to calculate said distance:

`d_(My)=y_M-y_J=4-3=1`
`d_(Mx)=X_J-X_M=6-(-3)=6+3=9_{}`

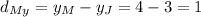
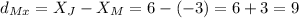
The distance between points J and M is 1 unit over the y-axis and 9 units over the x-axis, this is the same distance point K is from point M.

If you graph both points in the cartesian system and link them with a line, you'll see that point K is located in the fourth quadrant.

So to determine its coordinates, you have to add the calculated distance to the y- coordinate of M:

`y_K=y_M+d_(My)=4+1=5`

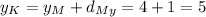
And subtract the distance over the x-axis to the x-coordinate of M

`x_K=y_M-d_(Mx)=-3-9=-12`

The coordinates of K are (-12,5)

The correct option is the first one.