Given:
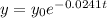
Where t is the time in years.
Initial amount = 300 g
Time, t = 18 years
Let's find the amount that will remain after 18 years.
Given that the function is an exponential decay function, we have:
Initial amount = y0
Final amount = y
time = t
To find the amount that will remain after 18 years, plug in 300 for y0 and 18 for t.
We have:

Therefore, to find the amount remaining after 18 years, we are to evaluate the function below;

ANSWER: D
