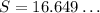Notice that the pyramid has four triangular sides and a square-shaped base.
To find the height of the triangles, notice that the slant height of the pyramid can be calculated using the Pythagorean Theorem, since it is the hypotenuse of a right triangle formed with the height of the pyramid and half the side of the square. Then, the slant heihgt of the pyramid, is:
![\sqrt[]{3^2+1^2}=\sqrt[]{9+1}=\sqrt[]{10}](https://img.qammunity.org/2023/formulas/mathematics/high-school/xlgcjfo6u8nmidawy8pd1vv0kctwhrvwp6.png)
The area of each triangular side is half its base times its height:
![\begin{gathered} A_T=(1)/(2)b* h \\ =(1)/(2)(2)(\sqrt[]{10}) \\ =\sqrt[]{10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/omyn5pz5cnzthoci2jiulh8ik20j8cw0ww.png)
The area of the base equals its side squared:
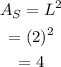
To find the total surface area of the pyramid, add four times the area of a triangular side plus the area of the base:
![\begin{gathered} S=4A_T+A_S \\ =4(\sqrt[]{10})+4 \\ =4\cdot\sqrt[]{10}+4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/8ivqy5bf9wgpvlvy2m6t0lrgw0mf3bas6v.png)
Use a calculator to find a decimal expression for the total surface area: