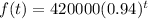Question

A manufacturing plant purchases new equipment for $420,000 which depreciates value at a rate of 6% annually.Write an equation for an exponential function f(t) that models the value of the equipment over time.f(t) =

Answer 1

Given:

The cost of new equipment = $ 420,000.

The depreciation rate is 6 % annually.

The variable t represents the time.

Aim:

We need to find the exponential function f(t) that models the value of the equipment over time.

Step-by-step explanation:

The exponential function f(t) is decay function.

Consider the exponential decay function.

`f(t)=a(1-r)^t`

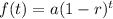
where a is the initial value and r is the decay rate.

The initial value = the cost of new equipment, a = 420,000.

The decay rate = the depriciation rate, r =6% =0.06.

Substitute a =420000 and r = 0.06 in the decay exponential function.

`f(t)=420000(1-0.06)^t`

`f(t)=420000(0.94)^t`

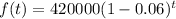
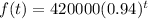
Final answer:

The equation for an exponential function f(t) that models the value of the equipment over time is

`f(t)=420000(0.94)^t`