Given the Absolute Value Function:

You need to remember that the form of an Absolute Value Function is:
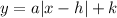
Where "h" is the x-coordinate of the vertex, and "k" is the y-coordinate of the vertex. If "a" is positive the function opens up, and if it is negative, the function opens down.
By definition:
- If "a" is positive, then the Range of the function is:
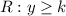
- If "a" is negative, the Range of the function is:
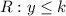
In this case, you can identify that:
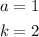
Therefore, you can determine that its Range is:
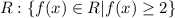
Hence, the answer is: Second option.