Question

Au-180 has a half life of 8 seconds. How much of a 60 gram sample will remain radioactive after 32 seconds?15 g3.75 g30 g7.5 g

Answer 1

Remember that the formula of half-life is the following:

`N(t)=N_0((1)/(2))^{(t)/(t2)},`

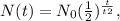
Where N(t) is the amount in grams, N(0) is the initial amount and t2 is the half-life in seconds.

Replacing the data that we have, which N(0) is 60 g and t2 is 8 seconds, we're going to obtain:

`N(t)=60((1)/(2))^{(t)/(8)},`

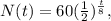
And the problem is asking for the amount of Au-180 in grams after 32 seconds, so t would be 32:

`\begin{gathered} N(32)=60((1)/(2))^{(32)/(8)}, \\ N(32)=3.7\text{5 g.} \end{gathered}`

The answer is that after 32 seconds, it will be 3.75 grams of Au-180.