Question

A section of an exam contains five true–false questions. A completed exam paper is selected at random, and the answers are recorded. Write each answer using fraction.a. Assuming the outcomes to be equally likely, find the probability that all answers are “True."b. Assuming the outcomes to be equally likely, find the probability that exactly three of the five answers is "False."c. Assuming the outcomes to be equally likely, find the probability that all the answers are the same.d. Assuming the outcomes to be equally likely, find the probability that at least one answer

Answer 1

Using the probability of binomial expereiment.

`\text{Prob}=nC_r(p)^r(q)^(n-r)`

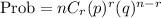
Since the outcome of true and false is equal as stated in the problem, the value of p and q is 0.5 each

and we have 5 questions, so n = 5

p = 0.5

q = 0.5

n = 5

a. Probability that all answers are "True"

Let's say all p are True, and all q are False

So we need 5 True's, so r = 5

`\begin{gathered} \text{Prob}=5C5(0.5)^5(0.5)^0 \\ =1(0.5)^5(1) \\ =0.5^5 \\ =0.03125 \end{gathered}`

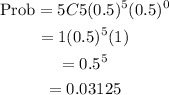
The probability is 0.03125

`\begin{gathered} 0.03125=(3125)/(100000) \\ =(3125)/(100000)/(3125)/(3125)=(1)/(32) \end{gathered}`

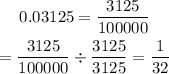
So the equivalent fraction is 1/32

b. Probability that exactly 3 are False's, it means that there are 2 True's

so r = 2

`\begin{gathered} \text{Prob}=5C_2(0.5)^2(0.5)^3 \\ =10(0.5)^2(0.5)^3 \\ =10(0.25)(0.125) \\ \text{Prob}=0.3125 \end{gathered}`

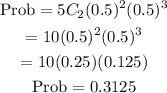
The probability is 0.3125

`\begin{gathered} 0.3125=(3125)/(10000) \\ =(3125)/(10000)/(625)/(625)=(5)/(16) \end{gathered}`

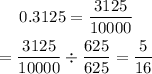
The equivalent fraction is 5/16

c. Probability that all answers are the same

Case 1, all answers are True, but we already have the value for this, in letter "a" which is 0.03125

Case 2, all answers are False, there must be 5 False's, so there are 0 True

Therefore, r = 0

`\begin{gathered} \text{Prob}=5C_0(0.5)^0(0.5)^5 \\ =1(1)(0.5)^5 \\ =0.03125 \end{gathered}`

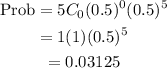
The probability will be the sum of 5 True's and 5 False's

Prob = 0.03125 + 0.03125 = 0.0625

`\begin{gathered} 0.0625=(625)/(10000) \\ =(625)/(10000)/(625)/(625)=(1)/(16) \end{gathered}`

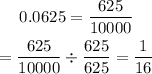
The equivalent fraction is 1/16

d. Probability that atleast one answer is False.

There are 5 cases which will satisfy this.

Case 1 : 1 False, 4 True

so r = 4

`\begin{gathered} \text{Prob}=5C4(0.5)^4(0.5)^1 \\ =5(0.0625)(0.5) \\ =0.15625 \end{gathered}`

Case 2 : 2 False, 3 True

so r = 3

`\begin{gathered} \text{Prob}=5C_3(0.5)^3(0.5)^2 \\ =10(0.125)(0.25) \\ =0.3125 \end{gathered}`

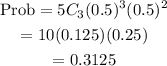
Case 3 : 3 False, 2 True

so r = 2

`\begin{gathered} \text{Prob}=5C_2(0.5)^2(0.5)^3 \\ =10(0.25)(0.125) \\ =0.3125 \end{gathered}`

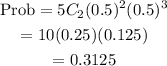
Case 4 : 4 False, 1 True

so r = 1

`\begin{gathered} \text{Prob}=5C1(0.5)^1(0.5)^4 \\ =5(0.5)(0.0625) \\ =0.15625 \end{gathered}`

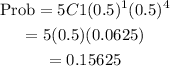
Last, Case 5 : 5 False, 0 True

But we already have the result for this in c. Case 2 which is 0.03125

The probability will be the sum of probabilities from Case 1 up to Case 5

Prob = 0.15625 + 0.3125 + 0.3125 + 0.15625 + 0.03125

Prob = 0.96875

`\begin{gathered} 0.96875=(96875)/(100000) \\ =(96875)/(100000)/(3125)/(3125)=(31)/(32) \end{gathered}`

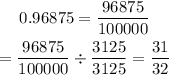
The equivalent fraction is 31/32