Question

Find the arean of the regular polygon. round your answer to the nearest tenth

Answer 1

The area of the hexagon is given as:

`A=(1)/(2)Pa`

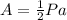
where P is the perimeter and a is the apothem.

Now, we need to notice that the we have the following triangle:

and we notice that x is half the length of each side of the hexagon.

From this triangle we notice that:

`\begin{gathered} \tan 60=(6)/(x) \\ x=(6)/(\tan60) \\ x=\frac{6}{\sqrt[]{3}} \\ x=\frac{6\sqrt[]{3}}{3} \end{gathered}`

Once we found x that means that each side has length :

`\frac{12\sqrt[]{3}}{3}`

Now, the perimeter is:

`6\cdot\frac{12\sqrt[]{3}}{3}=24\sqrt[]{3}`

Plugging this values and the apothem in the area formula we have that:

`A=(1)/(2)(24\sqrt[]{3})(6)=72\sqrt[]{3}=124.7`

Therefore the area is 124.7 squared inches