The area of the hexagon is given as:
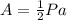
where P is the perimeter and a is the apothem.
Now, we need to notice that the we have the following triangle:
and we notice that x is half the length of each side of the hexagon.
From this triangle we notice that:
![\begin{gathered} \tan 60=(6)/(x) \\ x=(6)/(\tan60) \\ x=\frac{6}{\sqrt[]{3}} \\ x=\frac{6\sqrt[]{3}}{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/f3kpepjh9e37k0jjxwcqbetsceudjb6yx1.png)
Once we found x that means that each side has length :
![\frac{12\sqrt[]{3}}{3}](https://img.qammunity.org/2023/formulas/mathematics/college/asjofepagjh37r24ky0ibmsg7u9brvayu6.png)
Now, the perimeter is:
![6\cdot\frac{12\sqrt[]{3}}{3}=24\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/zbg1g02beiv318wefnblssb70ml7xxvvfr.png)
Plugging this values and the apothem in the area formula we have that:
![A=(1)/(2)(24\sqrt[]{3})(6)=72\sqrt[]{3}=124.7](https://img.qammunity.org/2023/formulas/mathematics/college/c10byxsps9wgt9xfaui0ymdo0r2v5pymqk.png)
Therefore the area is 124.7 squared inches