Question

I need help with this practice problem solving The subject for this is complex numbers and vectors Make sure to read the instructions in red

Answer 1

Given the following complex number:

`2√(3)-2i`

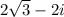
We will find the fourth root by the following formula:

`\begin{gathered} if,z=r(cos\theta+i*sin\theta) \\ so,\sqrt[n]{r}(cos(\theta+2\pi k)/(n)+i*sin(\theta+2\pi k)/(n)) \end{gathered}`

For the given number, we will find the fourth root

n = 4, k = 0, 1, 2, 3

First, we will convert the number from rectangular form to the polar form:

`z=2√(3)-2i=4(cos330+i*sin330)`

Apply the previous formula, the four roots will be as follows:

`\begin{gathered} k=0\rightarrow\sqrt[4]{4}(cos(330)/(4)+i*sin(330)/(4))=\sqrt[]{2}(cos82.5+i*sin82.5) \\ \\ k=1\rightarrow\sqrt[4]{4}(cos(330+90)/(4)+i*sin(330+90)/(4))=√(2)(cos105+i*sin105) \\ \\ k=2\rightarrow\sqrt[4]{4}(cos(330+180)/(4)+i*sin(330+180)/(4))=√(2)(cos127.5+i*sin127.5) \\ \\ k=3\rightarrow\sqrt[4]{4}(cos(330+270)/(4)+i*sin(330+270)/(4))=√(2)(cos150+i*sin150) \end{gathered}`