Given the following complex number:
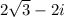
We will find the fourth root by the following formula:
![\begin{gathered} if,z=r(cos\theta+i*sin\theta) \\ so,\sqrt[n]{r}(cos(\theta+2\pi k)/(n)+i*sin(\theta+2\pi k)/(n)) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y98ewb8oho0d2x3z0e51hhxtftcyh6bdri.png)
For the given number, we will find the fourth root
n = 4, k = 0, 1, 2, 3
First, we will convert the number from rectangular form to the polar form:
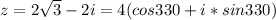
Apply the previous formula, the four roots will be as follows:
![\begin{gathered} k=0\rightarrow\sqrt[4]{4}(cos(330)/(4)+i*sin(330)/(4))=\sqrt[]{2}(cos82.5+i*sin82.5) \\ \\ k=1\rightarrow\sqrt[4]{4}(cos(330+90)/(4)+i*sin(330+90)/(4))=√(2)(cos105+i*sin105) \\ \\ k=2\rightarrow\sqrt[4]{4}(cos(330+180)/(4)+i*sin(330+180)/(4))=√(2)(cos127.5+i*sin127.5) \\ \\ k=3\rightarrow\sqrt[4]{4}(cos(330+270)/(4)+i*sin(330+270)/(4))=√(2)(cos150+i*sin150) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hpqlygmn0f841jwbsrq8o5srgugtzgbqoz.png)