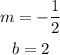The equation of a line in its slope-intercept form is
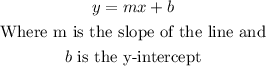
Then, to find the slope and the y-intercept of the given lines, you just have to take the equations to their slope-intercept form.
For point 4 b) you have

Therefore, the slope and the y-intercept of this equation are
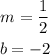
For point 4 c) you have

Therefore, the slope and the y-intercept of this equation are