Question

I invested $5000 between two accounts paying 7% and 9% annual interest respectively. If the total interest for a year was $370, How much was invested at each rate?

Answer 1

The given information is:

- The total amount invested was $5000

- The two accounts pay 7% and 9% respectively

- The total interest for a year was $370.

We need to write an equation that models the problem.

Let's set x= money invested in the first account and y =money invested in the second account, so:

`\begin{gathered} x+y=5000 \\ \text{ y in terms of x is:} \\ y=5000-x \end{gathered}`

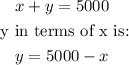
Now, the interest earned is given by the formula:

`\begin{gathered} 0.07x+0.09y=370 \\ \text{ Replace y in terms of x} \\ 0.07x+0.09(5000-x)=370 \end{gathered}`

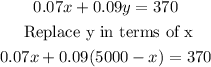
Now, let's solve for x:

`\begin{gathered} \text{ Apply the distributive property} \\ 0.07x+0.09*5000-0.09x=370 \\ 0.07x+450-0.09x=370 \\ 0.07x-0.09x=370-450 \\ -0.02x=-80 \\ \\ x=(-80)/(-0.02) \\ \\ x=4000 \end{gathered}`

Replace this value into the y formula, and find y:

`\begin{gathered} y=5000-4000 \\ y=1000 \end{gathered}`

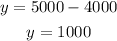
Therefore, you invested $4000 at a rate of 7% and $1000 at a rate of 9%.