The given information is:
- The total amount invested was $5000
- The two accounts pay 7% and 9% respectively
- The total interest for a year was $370.
We need to write an equation that models the problem.
Let's set x= money invested in the first account and y =money invested in the second account, so:
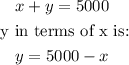
Now, the interest earned is given by the formula:
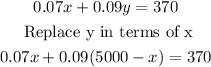
Now, let's solve for x:

Replace this value into the y formula, and find y:
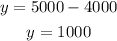
Therefore, you invested $4000 at a rate of 7% and $1000 at a rate of 9%.