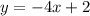Question

hi how do i , Find the equation of the line in slope intercept form that is perpendicular to the line 2x - 8y + 20 = 0 that goes through the point (-1, 6)

Answer 1

We have the following equation:

`2x-8y+20=0`

In order to locate the slope of this line equation, lets isolate the variable y. Then, by subtracting 2x and 20 to both sides, we have

`-8y=-2x-20`

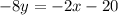
and by dividing both sides by -8, we obtain

`\begin{gathered} y=(-2x-20)/(-8) \\ y=-(2)/(-8)x-(20)/(-8) \\ y=(1)/(4)x+(5)/(2) \end{gathered}`

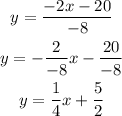
By comparing this result with the slope-intercept form

`y=mx+b`

we can see that the slope m of the given line equation is

`m=(1)/(4)`

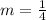
Since we need a perperdicular line, we need to compute the negative reciprocal of the slope m, that is,

`\begin{gathered} M\questeq-(1)/(m) \\ so \\ M=-(1)/((1)/(4))=-4 \end{gathered}`

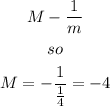
Then, the perpendicular line has the form

`\begin{gathered} y=Mx+b \\ \text{that is, } \\ y=-4x+b \end{gathered}`

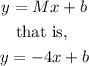
Finally, we can find the y-intercept b by substituting the coordinates of the given point (-1,6). It yields,

`6=-4(-1)+b`

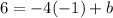
which gives

`\begin{gathered} 6=4+b \\ \text{then} \\ b=2 \end{gathered}`

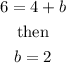
Therefore, the perpendicular line to 2x-8y+20=0 that goes throught the point (-1,6) is:

`y=-4x+2`