Question

Lynn uses this equation to model the growth of a bacteria culture. She let N represent the number of bacteria present after t hours of growth. N equals 100 e Superscript k t Baseline There were 400 bacteria present after 5 hours of growth.QuestionWhich is equal to the value of k?

Answer 1

Given:

There are given the equation:

`N=100e^(kt)`

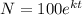
Step-by-step explanation:

From the given exponential function, N represents the number of bacteria and t represents the time.

Then,

According to the question, the value of N is 400 and the value of t is 5.

So,

Put the value of N and t into the above expression to find the value of k.

Then,

`\begin{gathered} N=100e^(kt) \\ 400=100e^(k(5)) \end{gathered}`

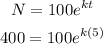
Then,

`\begin{gathered} 400=100e^(k(5)) \\ (400)/(100)=(100e^(5k))/(100) \\ 4=e^(5k) \end{gathered}`

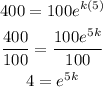
Then,

`\begin{gathered} 4=e^(5k) \\ 5k=ln(4) \\ k=(ln(4))/(5) \end{gathered}`

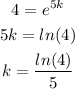
So,

The value of k is shown below:

`k=(ln(4))/(5)`

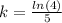
Final answer:

Hence, the correct option is D.