Given:
There are given the equation:
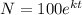
Step-by-step explanation:
From the given exponential function, N represents the number of bacteria and t represents the time.
Then,
According to the question, the value of N is 400 and the value of t is 5.
So,
Put the value of N and t into the above expression to find the value of k.
Then,
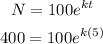
Then,
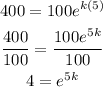
Then,
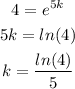
So,
The value of k is shown below:
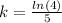
Final answer:
Hence, the correct option is D.