Question

Hi, can you help me answer this question please, thank you!

Answer 1

given the information on the picture, since we have that n*p is greater than 10, we can use a normal distribution.

We have that the critical value for 99% confidence level is 2.58.

Next, we can find the Standard Error with the following expression:

`SE=\sqrt[]{(p(1-p))/(n)}`

in this case we have the following:

`SE=\sqrt[]{(0.6\cdot0.4)/(160)}=00387`

then, according to the margin of error formula:

`ME=CV\cdot SE`

where CV is the critical value, we get:

`ME=2.58\cdot0.0387=0.099`

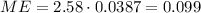
therefore, the margin of error is 0.099 which is a 9.9% error