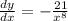Question

Finding a derivative: use the rule of differentiation to find the derivative of the functiony = 3/x^7

Answer 1

Given the function:

`y=(3)/(x^7)`

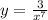
Let's use the rule of differentiation to find the derivative of the function.

To find the derivative using the rule of differentiation, we have:

Since 3 is constant with respect to x, we have:

`3(dy)/(dx)((1)/(x^7))`

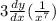
Apply the basic rule of exponents:

`3(d)/(dx)(x^(-7))`

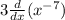
Differentiate using Power rule:

`\begin{gathered} 3(-7x^(-8)) \\ \\ =-21x^(-8) \end{gathered}`

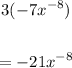
Apply the negative exponent rule:

`=-(21)/(x^8)`

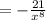
Therefore, the derivative of the function is:

`(dy)/(dx)=-(21)/(x^8)`

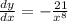
ANSWER:

`(dy)/(dx)=-(21)/(x^(8))`