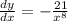Given the function:
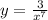
Let's use the rule of differentiation to find the derivative of the function.
To find the derivative using the rule of differentiation, we have:
Since 3 is constant with respect to x, we have:
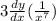
Apply the basic rule of exponents:
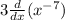
Differentiate using Power rule:
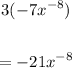
Apply the negative exponent rule:
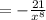
Therefore, the derivative of the function is:
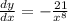
ANSWER: