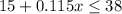Question

The cost of a car rental is 30$ per day plus 23 cents per mile. You are on a daily budget of 76$. Write and solve an inequality to find the greatest distance you can drive each day while staying within your budget. Use pencil and paper. Find 2 other two-step inequalities with the same solutions.

Answer 1

Let be "x" the greatest distance (in miles) you can drive each day while staying withing your budget.

You know that your daily budget is $76.

Then, using the information given in the exercise, you can set up the following inequality:

`30+0.23x\le76`

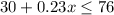
As you can notice, the sum of $30 per day and $0.23 per mile must be less than or equal to $76.

Solve for "x":

- Subtract 30 from both sides of the inequality:

`\begin{gathered} 30+0.23x\le76 \\ 30+0.23x-(30)\le76-(30) \\ 0.23x\le46 \end{gathered}`

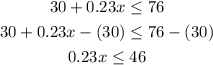
- Divide both sides of the inequality by 0.23:

`\begin{gathered} (0.23x)/(0.23)\le(46)/(0.23) \\ \\ x\le200 \end{gathered}`

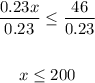
In order to find two other two-step inequalities with the same solution, you can multiply or divide the both sides of the original inequality by the same number. Then:

Inequality 1

`\begin{gathered} (2)(30+0.23x)\le(76)(2) \\ 60+0.46x\le152 \\ \end{gathered}`

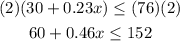
Inequality 2

`\begin{gathered} ((1)/(2))(30+0.23x)\le(76)((1)/(2)) \\ \\ 15+0.115x\le38 \end{gathered}`

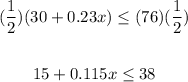
Answers

- You can drive at most 200 miles per day.

- Inequality 1:

`60+0.46x\le152`

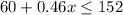
- Inequality 2:

`15+0.115x\le38`