For this problem, we use the sine law to compute the length of the missing sides:
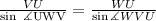
Recalling that the interior angles of a triangle add up 180 degrees we get:
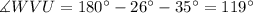
Substituting the angles and solving for the length of the missing sides we get:
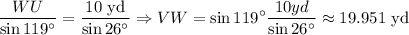
The height of the triangle with respect to the side WU is:
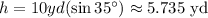
Finally, using the formula for the area of a triangle:
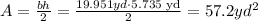
Answer: 57.2 square yards.