1 Answer

Andrea Moro · Answer 1 · 2023-05-02T07:06:44+0000

Remember that

The surface area of the given figure, is equal to the area of all its six faces

step 1

Find out the area of the base

The base is a rectangle of 19 in x 22 in

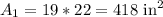
$A_1=19*22=418\text{ in}^2$

step 2

Find out the area of the top

The top is a rectangle of 13 in x 22 in

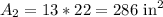
$A_2=13*22=286\text{ in}^2$

step 3

Find out the area of the two trapezoidal faces

$A_(3-4)=2[(1)/(2)(19+13)(14)]=448\text{ in}^2$

step 4

Find out the area of the two lateral rectangular faces

$A_(5-6)=2[22*16]=704\text{ in}^2$

therefore

The surface area is equal to

SA=418+286+448+704

Please log in or register to add a comment.