Hello there. To solve this question, we'll need to remember some properties about equation of lines.
First, a line in slope-intercept form has the equation y = ax + b, for some a, b constants. The constant a is called the slope of the line, while b is the intercept of the y-axis.
When two lines are parallel, they share the same slope, in this case, a.
We want to find a line that passes through the point (0, 4) and is parallel to the line described by y = 3x - 7.
With the first information, we plug in x = 0 and y = 4 in the equation of a line of the form y = ax + b
4 = a * 0 + b
Multiplying the terms, we have:
4 = b
So we know the line we're looking for have the form y = ax + 4
Now, remember that if two lines are parallel, they share the same leading coefficient. Therefore, a must be equal to 3.
The equation of this line in slope-intercept form will be:
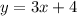
You can see those lines in the image I'll upload: