Solution:
The total number of cats up for adoption is
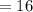
The number of male cats is
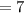
The number of female cats is
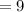
Since 5 cats are to be picked and he prefers only female cats, the probability will be
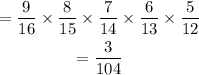
Hence,
The final answer is
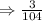
The SECOND OPTION is the right answer