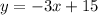To find the equation of the line in its slope-intercept form, you can find the slope of the line and then use the point-slope formula.
The formula for the slope is

In this case, you have
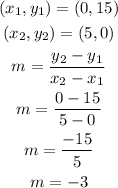
Now, the point-slope formula is
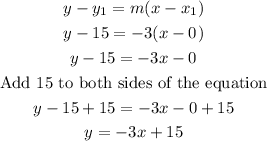
Therefore, the equation in slope-intercept form to represent this situation is