Answer: A
Given that:
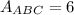
And the formula for finding the area of a triangle is
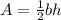
We can rewrite this as

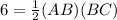
*Solve for BC
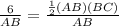
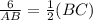
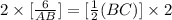
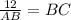
Now, given that BC = CD,
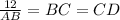
Given that BC and CD are equal, this would mean that:
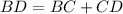

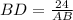
To find the Area of ACD, we will subtract the Area of ABC from the Area of ABD
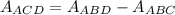
We can rewrite this as:
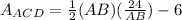
Evaluate

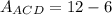
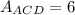
Therefore, the Area of ACD is 6.