Which function has the greater average rate over the interval [-2,-1]?x | f(x)---------2 | 10-1 | 80 | 61 | 4g(x) = {x}^(2) - 2x + 1

Question

Which function has the greater average rate over the interval [-2,-1]?x | f(x)---------2 | 10-1 | 80 | 61 | 4
`g(x) = {x}^(2) - 2x + 1`

Answer 1

First function,

F(x)

The find the greatest rate of change, you will find the slope over the given interval.

The slope of the function f(x) is m

`m\text{ = }\frac{y_2-y_1_{}_{}_{}}{x_2-x_1}`

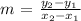
From the table,

x1 = -2, y1 = 10

x2 = -1, y2 = 8

`\begin{gathered} m\text{ = }\frac{8\text{ - 10}}{-1\text{ - (-2)}} \\ m\text{ = }\frac{-2}{-1\text{ + 2}} \\ m\text{ = }(-2)/(1) \\ m\text{ = -2} \end{gathered}`

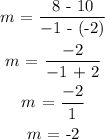
Second, function g(x)

`\begin{gathered} g(x)=-x^2\text{ - 2x + 1} \\ whenx_1=-2,y_{1\text{ }}=-(-2)^{2\text{ }}-\text{ 2(-2) + 1 = -4 + 4 + 1 = 1} \\ \text{when x}_2=-1,y_2=-(-1)^2\text{ - 2(-1) + 1 = -1 + 2 + 1 = 2} \\ \text{next, find the rate of change} \\ m\text{ = }\frac{2\text{ - 1}}{-1\text{ -(-2)}} \\ m\text{ = }\frac{1}{-1\text{ + 2}} \\ m\text{ = }(1)/(1) \\ m\text{ = 1} \end{gathered}`

Third function h(x)

`\begin{gathered} \text{From the graph of h(x)} \\ \text{when x}_1=-1interceptthecurveat0,therefore.y_1\text{ = 0} \\ \text{when x}_2\text{ = -2 intercept the curve at }3,therefore,y_2\text{ = 3} \\ m\text{ = }\frac{\text{3 - 0}}{-\text{ 1 -(-2)}} \\ m\text{ = }\frac{3}{-1\text{ + 2}} \\ m\text{ = }(3)/(1) \\ m\text{ = 3} \end{gathered}`

From the solution above, the function h(x) has the greatest average rate over the interval (-2, -1).

Final answer

h(x) has the greatest overage rate over interval [-2, -1]