First function,
F(x)
The find the greatest rate of change, you will find the slope over the given interval.
The slope of the function f(x) is m
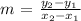
From the table,
x1 = -2, y1 = 10
x2 = -1, y2 = 8
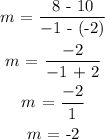
Second, function g(x)
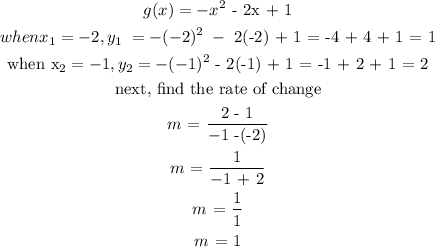
Third function h(x)

From the solution above, the function h(x) has the greatest average rate over the interval (-2, -1).
Final answer
h(x) has the greatest overage rate over interval [-2, -1]