Given:
Initial Amount, P = $1000
Rate of interest, r = 8% = 0.08
Number of years, t = ?
Number of compounding period, n = 2
Required: Time required to double the initial amount.
Step-by-step explanation:
The formula to find the compound amount is

Since, A is the double of initial amount, A = $2000
Substitute the given values into the formula.
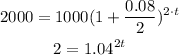
Take logarithm with base 1.04 on both sides.
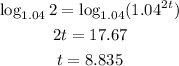
Thus, 8.835 years required to double the initial deposit.
Final Answer: 8.835 years required to double the initial deposit.