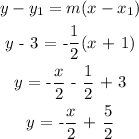Question

Find the equation of the line tangent to the function at the given point. y=x^3-2x^2+4 at (1,3)

Answer 1

The equation of the line tangent to the function at the given point is:

`y\text{ = -x + 4}`

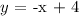
Explanation

The given equation is:

`y=x^3-2x^2\text{ + 4 }\ldots\ldots\ldots\ldots\ldots..\text{ (1)}`

Step 1: Determine the 1st derivative of the equation

`\begin{gathered} y=x^3-2x^2\text{ + 4} \\ \frac{d\text{ y}}{d\text{ x}}=y^{^(\prime)}=3x^(3-1)\text{ - 2}\cdot2x^(2-1)\text{ + }0 \\ y^{^(\prime)}=3x^2\text{ - 4x }\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots..\text{ (2)} \end{gathered}`

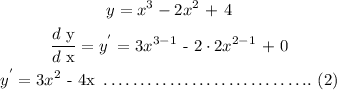
Step 2: To determine the slope (m) of the tangent line, insert the x-value (1) into the equation 2

`\begin{gathered} y^{^(\prime)}=3x^2\text{ - 4x} \\ y^{^(\prime)}=3(1)^2^{}\text{ - 4}(1) \\ y^{^(\prime)}=\text{ 3 - 4} \\ y^{^(\prime)}=\text{ - 1} \end{gathered}`

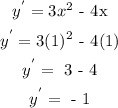
Step 3: use the point-slope formula to determine the equation of the line tangent to the given function at x = 1

`\begin{gathered} y\text{ - }y_1=m(x-x_1) \\ y\text{ - 3 = -1(x - 1)} \\ y\text{ - 3 = -x + 1} \\ y\text{ = -x + 1 + 3} \\ y\text{ = -x + 4 } \\ \end{gathered}`

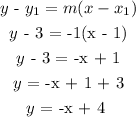
Hence, The equation of the line tangent to the function at the given point is:

`y\text{ = -x + 4 }`

=======================================================================

`y=(-3x+6)^{(1)/(2)}`

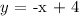
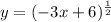
1. Take 1st derivative

`\frac{d\text{ y}}{d\text{ x }}=y^{^(\prime)}\text{ = }(1)/(2)(-3)(-3x+6)^{-(1)/(2)}`
`y^{^(\prime)}\text{ = -}(3)/(2)(-3x+6)^{-(1)/(2)}`

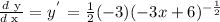
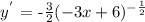
2. insert the x-value (-1) to determine the slope (m)

`\begin{gathered} y^{^(\prime)}\text{ = -}(3)/(2)(-3(-1)+6)^{-(1)/(2)} \\ y^{^(\prime)}\text{ = -}(3)/(2)(9)^{-(1)/(2)} \\ y^{^(\prime)}\text{ = -}(3)/(2)(\frac{1}{\sqrt[]{9}}) \\ y^{^(\prime)}\text{ = -}(3)/(2)\text{ }\cdot\text{ }(1)/(3) \\ y^{^(\prime)}\text{ = -}(1)/(2) \end{gathered}`

3. Now, determine the equation of the line tangent at (-1,3)

`\begin{gathered} y-y_1=m(x-x_1) \\ y\text{ - 3 = -}(1)/(2)(x\text{ + 1)} \\ y\text{ = -}(x)/(2)\text{ - }(1)/(2)\text{ + 3} \\ y\text{ = -}(x)/(2)\text{ + }(5)/(2) \end{gathered}`